사전 정보나 학습 없이 segmenatation하는 방법이 있을까

• Clustering is a problem of grouping similar data points

• Clustering is important for image processing and Image understanding

• Key challenge
  • 2 points or area를 similar 하게 만드는 것은 무엇일까
  • pairwise similarities 로 부터 모든 grouping 연산은 우찌 할 수 있을까

Idea

• non-parametric 접근법으로 density estimation 추론

• 한 local 에서 부터 density가 증가하는 방향으로 이동한다

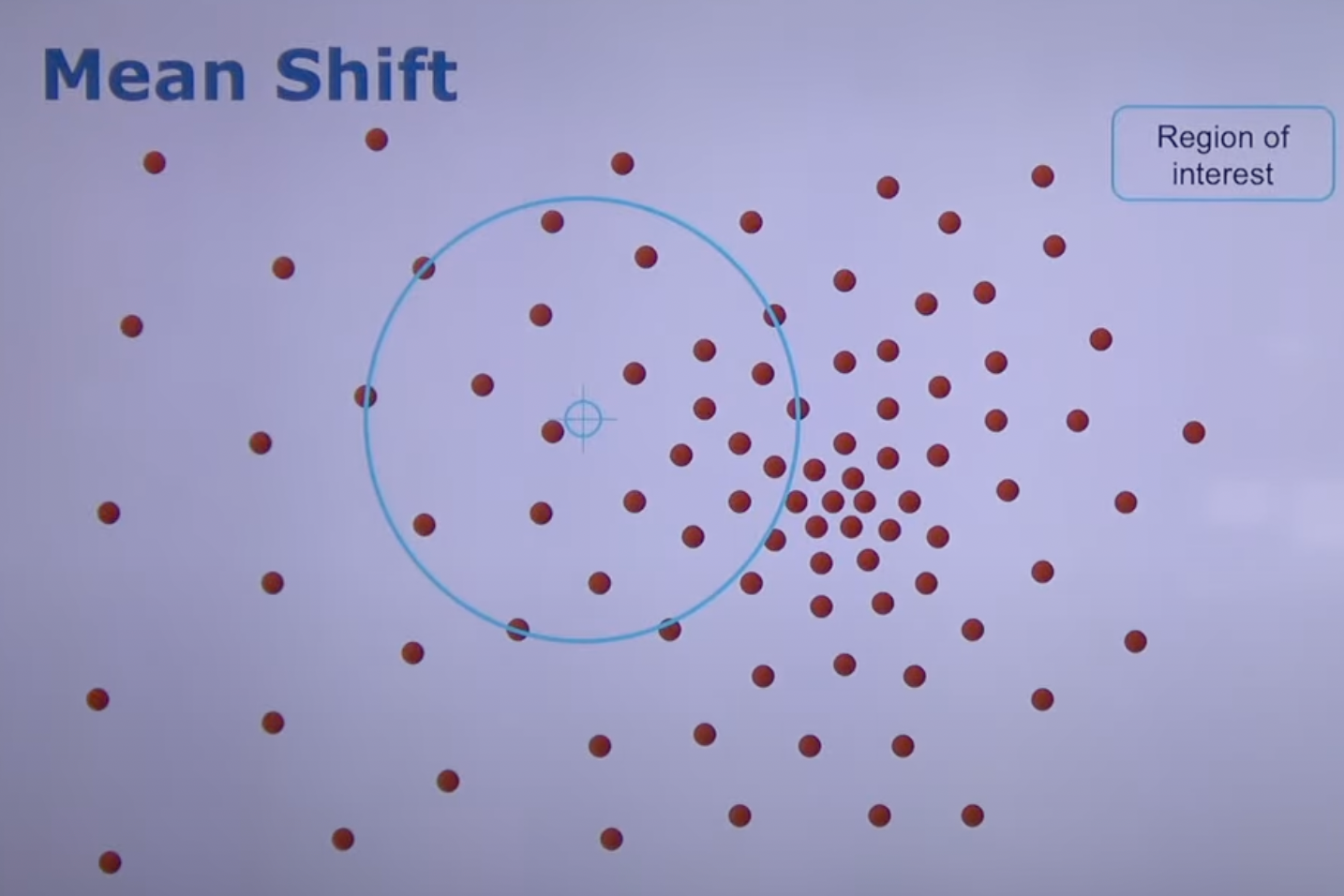
Density map에서 RoI를 설정하는 너무 작으면 그 지역에서 density가 어디가 높은지 모를 수 있기 때문에 조심
너무 크면 또 RoI가 하나밖에 없는 Unimodel이 될 수도 있다

이제 한 point에서 Kenel Func.을 통해 각 density로의 impact을 구하게 돼.

✨

Kernel Function
K(u) =$\frac{1}{\sqrt{2\pi}}e^{-u^2/2}$
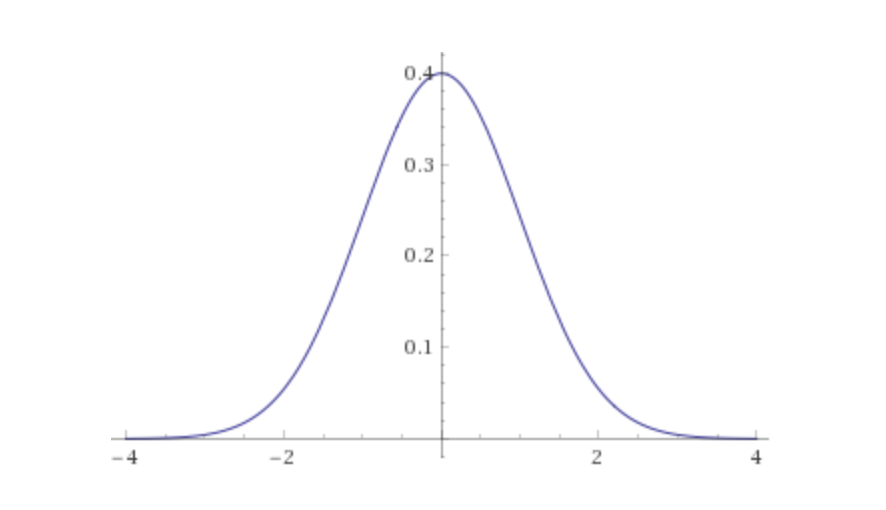
Gaussian Distribution을 따르는 이 함수는
중심으로 부터 멀어질 수록 가중치가 작아지는 함수.
중심으로 부터 특정 point까지의 거리를 나타냄.
이 함수를 통해 window의 중심을 찾아냄
만약 실제 170만큼 거리가 떨어져있으면 해당 point는 0.4개 정도 존재하고 169가 0.2정도 존재하고~ 이런 식으로 분포한다고 취급

x : point

x_m : region 안의 모든 point

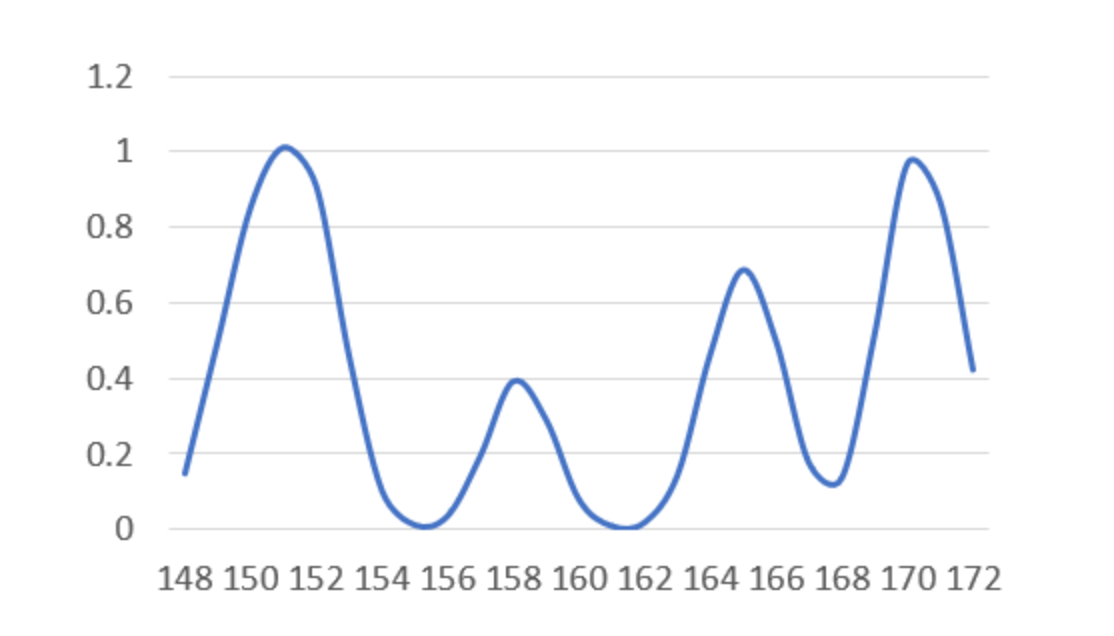
h : bandwidth. 커질 수록 아래의 그래프가 원만해지고 작을 수록 뾰족해짐

1. kernel과 bandwidth를 정한다
2. for each point
   1. point에 대한 window 설정
   2. window에 대한 mean 구하기
   3. 새로운 window 설정
   4. b~c 반복
3. Assign points that lead to nearby modes to the same cluster

• pixel의 color, gradient, texture 값에 따른 feature를 연산

• 각 feature, position마다 다른 kernel size

• Mean shift 진행

• 각 kernel size에 따라 window를 merge함

parameter가 적어서 효율적인 compute 가능

• Pros
  • 일반적인 segmentation으로 good
  • region의 모양과 크기가 유연하다
  • oulier에 강함

• Cons
  • kernel size를 미리 정해야 함
  • 고차원의 feature엔 적합하지 않음